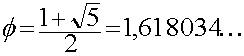A lo largo del tiempo los artistas han buscado una forma de proporción perfecta. Existe una fórmula eficaz, que permite dividir el espacio para lograr un efecto estético agradable. Esta teoría se denomina "La regla Áurea", también conocida como "divina proporción" o “numero áureo" representado con la letra griega Phi Ø.
Julián Maroto. Elena. Carbon / lienzo 146x114 cm.
Dividimos el alto del soporte por 1,618 medimos y marcamos este resultado es decir dos marcas por cada lado de forma que al unir las marcas trazamos dos lineas paralelas, hacemos la misma operación con el ancho, de este modo obtenemos cuatro puntos que guardan una proporción áurea, esta es la forma mas sencilla pero podemos seguir dividiendo cada cuadricula siguiendo el mismo procedimiento teniendo en cuenta el tema que vamos a pintar.
La regla de tres era una herramienta básica para los comerciantes del Quattrocento: servía para determinar las proporciones de capital, tierras, volumen de grano o cualquier otra clase de bienes que le correspondía a cada socio, heredero o copropietario ante un total determinado. Se la conocía entonces como regla de oro o llave del comerciante.
Una regla de tres famosa es la llamada Escala Armónica Pitagórica, que al modo renacentista se expresa: 6 8 9 12
Algunos arquitectos relacionaron la escala armónica pitagórica, utilizada para representar una escala musical, con el diseño visual proporcional. Segun Andrea Palladio (Andrea di Pietro della Góndola, Padua, 1508 - Vicenza, 1580 importante arquitecto veneciano) los espacios podrían ser diseñados "musicalmente" de acuerdo con esta escala: como el intervalo entre 6 y 12 es de una octava, entre 6 y 9 y entre 8 y 12 es de una quinta, entre 6 y 8 y entre 9 y 12 de cuarta y entre 8 y 9 de un tono, si se organizaban las dimensiones de las habitaciones de un edificio siguiendo esta serie, se estaría produciendo una armonía espacial como la que relaciona las notas musicales. La regla Áurea parecía una fórmula perfecta que cohesionaba las artes de la música, la pintura y la arquitectura.
El primero en hacer un estudio formal sobre el número áureo fue Euclides (300-265 a. C.) en "Los Elementos"
"Se dice que una línea recta está dividida entre el extremo y su proporcional cuando la línea entera es al segmento mayor como el mayor es al menor."
En 1509 el matemático y teólogo Luca Pacioli publica su libro De Divina Proportione en el que plantea las razones por las que considera apropiado denominar divino al Número áureo
En 1525, Alberto Durero (1471-1528) publica Instrucción sobre la medida con regla y compás de figuras planas y sólidas donde describe cómo trazar la espiral basada en rectángulos áureos (cuyos lados están en proporción áurea, es decir, el cociente entre su lado mayor y su lado menor es el número Phi) ,que se conoce como “espiral de Durero”.
El astrónomo Johannes Kepler (1571-1630), en Mysterium Cosmographicum desarrolló un modelo Platónico del Sistema Solar utilizando los sólidos platónicos, y se refirió al número áureo en términos grandiosos:
“La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras; el otro, la división de una línea entre el extremo y su proporcional. El primero lo podemos comparar a una medida de oro; el segundo lo debemos denominar una joya preciosa”
“La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras; el otro, la división de una línea entre el extremo y su proporcional. El primero lo podemos comparar a una medida de oro; el segundo lo debemos denominar una joya preciosa”
Una sección áurea es una división en dos de un segmento según proporciones dadas por el número áureo. La longitud total a + b es al segmento más largo a como a es al segmento más corto b.
(a + b) / a = a / b
Para obtener el valor de a a partir de esta razón considere lo siguiente: Siendo 1 la longitud del segmento más corto b y la de a sera x.
(1 + x) / x = x / 1
Para que estos segmentos cumplan con la razón áurea deben cumplir que: Multiplicando ambos lados por x y reordenando:
x2 - x - 1 = 0
Mediante la fórmula general de las ecuaciones de segundo grado se obtienen las dos soluciones de la ecuación, la solución positiva se representa por el símbolo Ø y su valor es 1,61803..., es el valor del número áureo o Phi.
Julián Maroto. Sonia pintando oleo/lienzo 146x114 cm.
La sucesión de Fibonacci
Consideremos la siguiente sucesión de números: 1, 1, 2, 3, 5, 8, 13, 21, 34...Cada número se obtiene sumando los dos que le preceden.
Esta sucesión es la llamada "sucesión de Fibonacci" (Leonardo de Pisa 1170-1240).Los cocientes entre dos números de la sucesión,1/1 ; 2/1 ; 3/2 ; 8/5; 13/8 ; 21/13... se aproximan más y más al número áureo (1'61803...).
La secuencia de Fibonacci se puede encontrar en la naturaleza, la flor del girasol, por ejemplo, tiene veintiuna espirales que van en una dirección y treinta y cuatro que van en la otra; ambos son números consecutivos de Fibonacci. La parte externa de una piña tiene espirales que van en sentido de las manecillas del reloj y otras que lo hacen en sentido contrario, y la proporción entre el número de unas y otras espirales tiene valores secuenciales de Fibonacci. En las curvas de la concha del nautilus, cada nueva circunvolución completa cumplirá una proporción de 1: 1,618, si se compara con la distancia desde el centro de la espiral precedente.
La secuencia de Fibonacci se puede encontrar en la naturaleza, la flor del girasol, por ejemplo, tiene veintiuna espirales que van en una dirección y treinta y cuatro que van en la otra; ambos son números consecutivos de Fibonacci. La parte externa de una piña tiene espirales que van en sentido de las manecillas del reloj y otras que lo hacen en sentido contrario, y la proporción entre el número de unas y otras espirales tiene valores secuenciales de Fibonacci. En las curvas de la concha del nautilus, cada nueva circunvolución completa cumplirá una proporción de 1: 1,618, si se compara con la distancia desde el centro de la espiral precedente.
Salvador Dalí , influenciado por las obras de Matila Ghyka , utiliza explícitamente la proporción áurea en su obra maestra El sacramento de la Última Cena. Las dimensiones del lienzo forman un rectángulo áureo. Un gran dodecaedro, en perspectiva cuyos vertices aparecen en proporción áurea entre sí, se suspende por encima y por detrás de Jesús y domina la composición.
El compositor Bela Bartok en su Música para cuerdas, percusión y celesta utiliza los intervalos 1:2:3:5:8:5:3:2:1 en la progresión del xilófono.
El compositor francés Erik Satie utilizó la proporción áurea en varias de sus piezas, incluyendo Melodías de la Rose + Croix.
El compositor francés Erik Satie utilizó la proporción áurea en varias de sus piezas, incluyendo Melodías de la Rose + Croix.
En 2010, la revista Science informó de la pesencia el número áureo en la escala atómica en la resonancia magnética de las formaciones de cristales niobato de cobalto.
Varios investigadores han propuesto las conexiones entre la proporción áurea y el genoma humano ADN.
Leonardo da Vinci y El Hombre de Vitruvio
El hombre de Vitrubio es un ejemplo del enfoque de Leonardo vinculando la arquitectura con el cuerpo humano, un aspecto de su interpretación de la naturaleza y del lugar de la humanidad en el "plan global de las cosas". Para Leonardo, el hombre era el modelo del universo, este dibujo representa las proporciones que podían establecerse en el cuerpo humano, la proporción áurea por ejemplo.
“Vitrubio el arquitecto, dice en su obra sobre arquitectura que la naturaleza distribuye las medidas del cuerpo humano como sigue: que 4 dedos hacen 1 palma, y 4 palmas hacen 1 pie, 6 palmas hacen 1 codo, 4 codos hacen la altura del hombre. Y 4 codos hacen 1 paso, y que 24 palmas hacen un hombre; y estas medidas son las que él usaba en sus edilicios. Si separas la piernas lo suficiente como para que tu altura disminuya 1/14 y estiras y subes los hombros hasta que los dedos estén al nivel del borde superior de tu cabeza, has de saber que el centro geométrico de tus extremidades separadas estará situado en tu ombligo y que el espacio entre las piernas será un triángulo equilátero. La longitud de los brazos extendidos de un hombre es igual a su altura. Desde el nacimiento del pelo hasta la punta de la barbilla es la décima parte de la altura de un hombre; desde la punta de la barbilla a la parte superior de la cabeza es un octavo de su estatura; desde la parte superior del pecho al extremo de su cabeza será un sexto de un hombre. Desde la parte superior del pecho al nacimiento del pelo será la séptima parte del hombre completo. Desde los pezones a la parte de arriba de la cabeza será la cuarta parte del hombre. La anchura mayor de los hombros contiene en sí misma la cuarta parte de un hombre. Desde el codo a la punta de la mano será la quinta parte del hombre; y desde el codo al ángulo de la axila será la octava parte del hombre. La mano completa será la décima parte del hombre; el comienzo de los genitales marca la mitad del hombre. El pie es la séptima parte del hombre. Desde la planta del pie hasta debajo de la rodilla será la cuarta parte del hombre. Desde debajo de la rodilla al comienzo de los genitales será la cuarta parte del hombre. La distancia desde la parte inferior de la barbilla a la nariz y desde el nacimiento del pelo a las cejas es, en cada caso, la misma, y, como la oreja, una tercera parte del rostro».
Traducción del texto que acompaña al Hombre de Vitruvio de Leonardo da Vinci. El dibujo fue originalmente una ilustración para un libro sobre las obras de Vitruvio (Marcus Vitruvius Pollio) arquitecto romano del siglo I a.c. que en época de Augusto escribió los diez tomos de su obra De architectura, que trata de la construcción hidráulica, de cuadrantes solares, de mecánica y de sus aplicaciones en arquitectura civil e ingeniería militar.